다이나믹프로그래밍2 - Optimal substructure

GeeksforGeeks의 글을 해석한 포스트 입니다.

Optimal Substructure Property in dynamic Programing / DP-2

이전 글에서 살펴 본것 처럼, 다음은 다이나믹 프로그래밍을 사용해서 풀수 있는 문제의 특성이다.

1) Overlapping Subproblems

2) Optimal Substructure

먼저 이전 글에서 첫번째 특성은 알아 보았다. 다음으로 두번째 속성에 대해서 알아보도록 하자

2) Optimal Substructure: 부문문제의 최적의 솔루션을 사용해서 주어진 문제의 최적의 해를 구할 수 있다면 이를 최적의 하부구조 속성이라고 한다.

예를 들어 최소 길이 문제는 Optimal substructure 속성을 따른다.

만약에 노드 x가 시작점 u에서 도착점 v로 가는 최단경로상에 있다면, 최단 경로 u-v는 최단경로 u-x와 x-v의 조합이다. 모든 최단 경로를 구하는 플로이드-와샬, 벨만-포드 알고리즘도 다이나믹 프로그래밍의 예제이다.

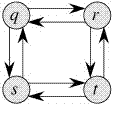
반면에 최장경로 문제는 Optimail Substructure 속성을 가지고 있지 않다. 여기서 최장경로란 두 노드 사이의 최장 단순 경로를 말한다.(사이클이 없는 경로). CLRS 책에서 추어진 가중치가 없는 그래프를 고려해보자. q-t의 최장 경로가 존재한다. q-r-t, q-s-t. 최단 경로와 달리, 최장경로는 Optimal substructure 의 특성이 없다. 예를 들어, 최장경로 q-r-t는 최장 경로 q-r과 r-t의 조합이 아니다. 왜냐하면 최장경로 q-r은 q-s-t-r 이고 최장경로 r-t는 r-q-s-t이기 때문이다.

이제 앞으로의 다이나믹 프로그래밍 포스트에서 더많은 문제에 대해서 다루도록 하자.