다익스트라 최단거리 알고리즘

다익스트라 최단거리 알고리즘

geeksforgeeks - Dijkstras shortest path algorithm 을 번역한 글입니다.

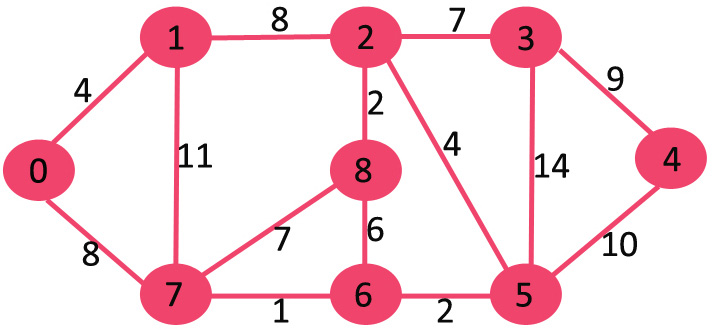
그래프와 그래프 속에 시작점(source vertex)이 주어진다면, 그래프안에서 시작 정점으로부터 모든 정점까지의 가장 짧은 거리를 찾는 알고리즘

다익스트라의 알고리즘은 프림의 최단 신장트리 알고리즘과 닮았다. 프림의 최단 스패닝트리(Minimum spanning tree - MST)처럼, 주어진 시작점을 루투로 하여 최단 길이 트리(Shortest path tree-SPT)를 만들 것이다. 알고리즘의 모든 스탭에서 소스로부터 가장짧으면서 아직 포함되지 않은 set에 있는 정점을 찾을 것이다.

다음은 다익스트라 알고리즘에서 가장 짧은 길을 찾기위한 자세한 step이다.

알고리즘

1) SPT에 포함되는 정점을 추적하기 위한 sptSet을 만든다. 즉 그 정점의 최단거리는 계산되어 결정되었다. 처음에 이 set은 비었다.

2) 그래프의 모든 정점에 거리(가중치) 값을 준다. 모든 거리는 처음에 무한대로 설정한다. 그리고 source 정점에는 0 값을 주어 처음에 선택되도록 한다.

3) 모든 정점이 sptSet에 포함될 때 까지 반복한다.

a) 아직 sptSet에 포함되지 않았고 가장 짧은 길이를 갖진 정점 u를 선택한다.

b) 이를 sptSet에 포함한다.

c) 정점 u에 인접한 모든 정점의 거리를 업데이트한다. 정점의 거리를 업데이트하기 위해, 모든 정점을 반복한다. 모든 정점 v에 대해서, 정점 u의 값과 u-v 간선의 가중치의 합이 정점 v의 값보다 작다면 정점 v의 거리 값을 갱신한다.

다음 예제를 이해해 보자.

sptSet은 비어있으며, 모든 정점에 무한대 값을 할당한다. {0, INF, INF, INF, INF, INF, INF, INF, INF}(정점 0은 시작점이고, INF는 무한대를 의미한다.) 다음으로 가장작은 거리값을 가진 정점을 선택한다. 정점 0이 선택되면 이를 sptSet에 넣는다. 이제 sptSet은 {0}이 된다. 점점 0을 sptSet에 포함 시킨 후, 0에 인점한 정점들의 거리를 갱신한다. 0에 인접한 정점은 1과 7이다. 각각의 정점의 거리는 '4'와 '8'로 갱신된다. 다음의 서브그래프는 거리가 결정된 정점과 그 거리 값을 보여준다. SPT에 포함된 정점은 초록색으로 보여진다.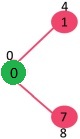

다음으로 아직 SPT에 포함되지 않은 정점중 거리가 가장 짧은 정점을 선택한다. 정점 1이 선택되고 sptSet에 포함한다. 이제 sptSet은 {0,1}이 된다. 다시 정점 1에 인접한 정점의 거리를 갱신한다. 정점 2의 거리 값이 12가 된다.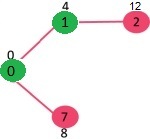

다시 가장 짧은 거리값을 가진 정점을 선택한다. 정점 7이 선택된다. 이제 sptSet은 {0,1,7}이 된다. 다시 7과 인점한 정점의 거리를 갱신한다. 정점 6과 8이 갱신된다.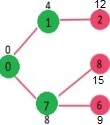

아직 SPT에 포함되지 않은 정점을 선택한다. 정점 6이 선택된다. (sptSet{0,1,7,6}). 정점 6과 인접한 정점의 거리를 업데이트한다. 정점 5와 8이 갱신된다.

모든 정점이 sptSet에 포함될때 까지 위의 과정을 반복한다. 결과적으로 다음과 같은 SPT를 얻을 수 있다.

특징

• 모든 정점을 서치해야하며, 모든 정점이 연결되어 있다면, O(V^2)의 시간이 든다.

• 구현할 때 우선순위 큐를 사용한다면 최단 거리인 정점을 쉽게 찾을 수 있다.

• 음의 가중치가 있다면 서클이 생기기때문에 값을 구할 수 없다.

• 알고리즘 접근방법중 그리드 알고리즘에 해당된다.

그래프 최단거리 알고리즘

• 하나의 정점에서 모든 정점까지의 최단거리 - 다익스트라

• 음의 값이 있을때 하나의 정점에서 모든 정점까지의 최단거리 - 벨만포드

• 모든 정점간의 최단거리 - 플루이드

---